#** you can always use https://scikit-learn.org for details on any of the below topics
#basic imports
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import os#to locate and read files
#other imports we can do whenever needed
#loading all the .csv's using os
filenames = os.listdir(dataFolder)
for file in filenames:
if file.endswith('csv'):
#load file or do something
#also you can do something like this
filenames = [file for file in os.listdir(filepath) if file.endswith('.csv')]
#after you have read the file few things you should do
data.shape#prints the shape row vs columns
data.describe()#gives an overview of the numerical columns
data.head()#prints the first five rows so that you can get an idea of what data looks like
data.info()#this also you can do, this will give you non null count of the columns and there datatype
data.apply(lambda x : sum(x.isnull()))#this will give you number of null values of each columns
#to get the numerical columns
num_cols = Data.describe().columns#as describe only gives stats on numerical columns, similarly you can use describe(include=['O']) for string or other columns
#train test split, if your data is not having training and testing data seperate, you can do the split yourself
#before you do your train test split you need to seperate your explanatory and dependent variable (your X and y)
y = data['Survived']
X = data.drop('Survived', axis=1)#we are using titanic data set here, here survived is the dependent variable
#other way to do the above X, y seperation is
y = data.pop('Survived')#it will pop out the Survived column from original data changing the original data and assign it to y
X = data#as survived(y) column is popped out the remaining is X
y.shape, X.shape#you can print the shapes of X and y to cross check
#now you can do the train test split
from sklearn.model_selection import train_test_split
#here stratify=y means y values will be equally representative in both train and test set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state=42, stratify=y)
#now as we have data some preprocessing needs to be done to feed the data into the algorithm
#we treat out test data as seperate as we have not seen it, we do our preprocessing on train data and then apply those preprocessing to test data based on train data
#getting unique count of variables
X_train.nunique()#or we can use X_train.apply(lambda x : x.nunique())
#it will output all the variable and there unique count, from here we can see how many variable have less distict values and then we can check for categorical variables
#for categorical variables we can do one hot encoding using pd.get_dummies,
#also we need to make sure that all the categories in the training data is also in test data else we will get unequal number of columns and the algo will fail
#droping unwanted cols based in unique count, if columns is an id column or a string column with most of the values as distict we can drop those
X_train.drop('PassengerId', inplace=True, axis=1)
X_test.drop('PassengerId', inplace=True, axis=1)
X_train.drop('Ticket', inplace=True, axis=1)
X_test.drop('Ticket', inplace=True, axis=1)
#imputing null values
#first thing you should always impute the null values as many other preprocessing algos might not work on null data
#in out data we have two columns with some missing data, one is Age, other is Cabin
#from printing the null count we noticed that Cabin has most of the values as null, so we can simply drop this column both from test and train
X_train.drop('Cabin', inplace=True, axis=1)
X_test.drop('Cabin', inplace=True, axis=1)
#now we have to impute the null values of column Age
#there are few ways to impute values
#you can use fillna and fill it will mean to median value
value_to_fill = X_train['Age'].median()
#or
value_to_fill = X_train['Age'].mean()
#and then use
X_train.fillna(value_to_fill)#similar you can do for test data, generally we use the train data values to impute the test data also
#or you can use the imputer from skearn.preprocessing
from sklearn.preprocessing import Imputer
imputer = Imputer(strategy='mean')#here we are filling with mean values
imputer.fit()
imputer.fit(X_train['Age'].values.reshape(-1,1))#here we have to reshape as we are only fitting a single colums and it expects a 2d data structure
#to check the value which will be imputed we can do
imputer.statistics_#returns the mean value as we chose strategy='mean' this values will be same as X_train['Age'].mean()
#now we can use the fitted value to impute the values using transform
X_train['Age'] = imputer.transform(X_train['Age'].values.reshape(-1,1))
#here we fitted and transformed seperately as we can use the imputer which we get after fitting to transform the test data also
#** the above mentioned is generally the way we do for most other preprocessing
#if we dont want to do that we have a single fucntion fit_transform which we can use to do it in single line
X_test['Age'] = imputer.transform(X_test['Age'].values.reshape(-1,1))#here we are using the same imputer to transform the test data also
#other ways to impute data is to treat the missing data column as dependent variable and fit a model on the non null values of that column
#and then use that model to predict the null values of that column, we generally use KNN (nearest neighbour) for this
#also you can use some other imputation packages which will do this for you
#also you can define your own way which makes more sense to you to fill the null values one such logic we will use here
#the logic for imputing data which we are going to use here is
#as from names column we can see names have Mr. Mrs. Miss Master, we can extract that data from name column and then find the median in each group and then use this for imputation
#we creater one more columns based on Master Header for both train and test
X_train['Name_Header'] = X_train['Name'].str.extract(r'(Mr\.|Miss\.|Mrs\.|Master\.)')
X_test['Name_Header'] = X_test['Name'].str.extract(r'(Mr\.|Miss\.|Mrs\.|Master\.)')
#we see now that we have some null values in our Name_Header, as those names do not have any of Mr/Mrs/Master/Miss
#to fill those nulls we can simple put Mr. for Males and Mrs. for Females
X_train['Name_Header'].fillna(X_train.loc[X_train['Name_Header'].isnull(),'Sex'], inplace=True)
X_test['Name_Header'].fillna(X_test.loc[X_test['Name_Header'].isnull(),'Sex'], inplace=True)#we are filling the values from Sex columns to NaN's in Name_Header
mapping = {'male':'Mr.', 'female':'Mrs.','Mr.':'Mr.','Miss.':'Miss.','Master.':'Master.','Mrs.':'Mrs.'}
#creat a dictionary which will be used to map male to Mr and female to Mrs, also we need all the other values in the mapping otherwise those values will be filled as null
X_train['Name_Header'] = X_train['Name_Header'].map(mapping)#using the above mapping as we want Mr and Mrs not male and female in Name_Header column
X_test['Name_Header'] = X_test['Name_Header'].map(mapping)
#the above is one way to do it may be not very efficient but you can see the working of map
#now drop the original Name columns
X_train.drop('Name', inplace=True, axis=1)
X_test.drop('Name', inplace=True, axis=1)
#now we will impute the null values for column Age based on median value in each group for Name_Header
X_train['Age'] = X_train.groupby('Name_Header')['Age'].transform(lambda x: x.fillna(x.median()))
X_test['Age'] = X_test.groupby('Name_Header')['Age'].transform(lambda x: x.fillna(x.median()))#you can also use the grouped values from train data, depending on the scenario
X_train['Embarked'].fillna(X_train['Embarked'].mode()[0], inplace=True)#filling few null in Embarked using mode, as we can not use median ot mean for string values
#X_train['Embarked'].mode()[0] returns the mode value, if you write only X_train['Embarked'].mode() it returns a series and the fillna function wont work with it
['Fare'] = X_test.groupby('Name_Header')['Fare'].transform(lambda x: x.fillna(x.mean()))#filling the null value in Fare column in test data
#now all the null values are filled and we have zero nulls in each column
#one hot encoding, or creating dummy variables, and Label Encoding
#most machine learning algo dont work very well with categorical variables so we can create dummy variable
#e.g. if we have 3 distinct values, we ca represnt them as 00, 10, 01 using two variable or we can use three variable for each values and the one having 1 is the value for that row
#when we create dummy variable for a column we create as many columns as the number of distinct values in our columns
#some minute difference between one hot encoding and get_dummies
#OneHotEncoder cannot process string values directly. If your nominal features are strings, then you need to first map them into integers
#pandas.get_dummies is kind of the opposite. By default, it only converts string columns into one-hot representation, unless columns are specified
#sometimes some algorithms can handle cateorical variable just fine, in that case you don't need to do the one hot encoding, all you can do is use LabelEncoder
#**also when our varible is ordinal like small<medium<big we use LabelEncoder but when we have something like cat dog rat we can't say cat>dog>rat so we use one hot encoding
#also we can use LabelEncoder if we have a binary variable like Male/Female
from sklearn.preprocessing import LabelEncoder
LE = LabelEncoder()#defining a label encoder
LE.fit(X_train['Sex'])#fitting only on the train data as we want the same encoding for test as we have for train
X_train['Sex'] = LE.transform(X_train['Sex'])#encoding train data as per train data fit
X_test['Sex'] = LE.transform(X_test['Sex'])#encoding train data as per train data fit just be sure that if we are using 1 for male in train same should be for test
#now creating dummy variables, also must remember that all the values of a variable should be present in both train and test data else we will have unequal number of columns
#one solution is that we can concat the two data and then create dummy variables or we can use one hot encoder from sklearn
#for us we have all the values on both train and test so we can simply use pd.get_dummies on both train and test
columns_to_dummy = ['Pclass','Embarked','Name_Header']
for col in columns_to_dummy:
X_train = pd.concat([X_train, pd.get_dummies(X_train[col], prefix=col)], axis=1)
X_test = pd.concat([X_test, pd.get_dummies(X_test[col], prefix=col)], axis=1)#creating dummies and concatinating, axis=1 means add as columns
X_train.drop(columns_to_dummy, axis=1, inplace=True)
X_test.drop(columns_to_dummy, axis=1, inplace=True)#droping the original cols
#for some algorithms we might need to scale the data in order to run the algorithm more effectively, we can do that using below methods depending on the problem
from sklearn.preprocessing import StandardScaler#z = (x - mu) / sigma, mu=mean, sigma=standard deviation
from sklearn.preprocessing import MinMaxScaler#z = (x - min(x)) / (max(x) - min(x))
from sklearn.preprocessing import Normalizer#not sure
#**many of the above steps might not be necessary and may or may not affect the performance of the model
#also they can be performed in many different ways
#we followed many steps just for tutorial purpose and to give you an idea on how to approach a problem
#usually we do may hit and trials and see if the extra steps done in preprocessing are really worth it
#but some steps are necessary like doing encoding as most models require numerical data or imputing as many models can't work with null values etc
#feature engineering generally helps but creating unwanted features may also degrade the model
#now for our problem the data is prepared and now we can proceed to apply algorithms
#as our goal is to predict wheather the passenger survived or not either 1 or 0, its a classification problem and as we have labelled data its a supervised learning problem
#which mean our model will learn based on the data and labels and then apply that learning to predict the labels of test data
#a general thing for all the models will be importing the model, fitting the data and then making predictions on the test data
#below we will be fitting just some basic models without any tuning (** hyperparameter tuning tends to improve the model) and check the score
#further we will explore each model in detail coming forward
#model1 - logistic regression
from sklearn.linear_model import LogisticRegression
LogR = LogisticRegression()
LogR.fit(X_train, y_train)
predictions = LogR.predict(X_test)
predictFrame = pd.DataFrame({'PassengerId':pd.read_csv(r'..\..\..\\tita\\test.csv')['PassengerId'],'Survived':predictions})#create a dataframe of the predictions
predictFrame.to_csv(r'..\..\..\\tita\\logisticBasic.csv', index=False)#save to csv to upload to kaggle as we don't have the original output
#the output score comes to be 0.78468
#model2 - decision tree
from sklearn.tree import DecisionTreeClassifier
Detree = DecisionTreeClassifier()
Detree.fit(X_train, y_train)
predictions = Detree.predict(X_test)
#the output score comes to be 0.65071
#model3 - extra tree
from sklearn.ensemble import ExtraTreesClassifier
Extree = ExtraTreesClassifier()
Extree.fit(X_train, y_train)
predictions = Extree.predict(X_test)
#the output score comes to be 0.73205
#model4 - random forest
from sklearn.ensemble import RandomForestClassifier
RandF = RandomForestClassifier()
RandF.fit(X_train, y_train)
predictions = RandF.predict(X_test)
#the output score comes to be 0.74641
#model5 - XGB - extreme gradient boosting
from xgboost import XGBClassifier
XGB = XGBClassifier()
XGB.fit(X_train, y_train)
predictions = XGB.predict(X_test)
#the output score comes to be 0.77990
#now i have got the actual score which i got from the web now i can use those to score my algos
actualpredictions = pd.read_csv(r'..\..\..\\tita\\perfectScore.csv')['Survived'].values#actual answers for titanic data set
#one way of getting score of a simple binary problem is using numpy array
1-abs(actualpredictions-predictions).mean()#this will give me the accuracy score
#we can do the same using accuracy score
from sklearn.metrics import accuracy_score
accuracy_score(actualpredictions, predictions)#this will give us the same output as above
#model6 - Adaboost
from sklearn.ensemble import AdaBoostClassifier
Ada = AdaBoostClassifier()
Ada.fit(X_train, y_train)
predictions = Ada.predict(X_test)
#the output score comes to be 0.765550
#model7 - Gradient Boosting
from sklearn.ensemble import GradientBoostingClassifier
GBM = GradientBoostingClassifier()
GBM.fit(X_train, y_train)
predictions = GBM.predict(X_test)
#the output score comes to be 0.78468
#model8 - KNN, nearest neighbor
from sklearn.neighbors import KNeighborsClassifier
KNN = KNeighborsClassifier()
KNN.fit(X_train, y_train)
predictions = KNN.predict(X_test)
#the output score comes to be 0.6722
#model9 - SGD, stochastic gradient descent
from sklearn.linear_model import SGDClassifier
SGD = SGDClassifier()
SGD.fit(X_train, y_train)
predictions = SGD.predict(X_test)
#the output score comes to be 0.67942
#model10 - Gaussian Naive Bayes
from sklearn.naive_bayes import GaussianNB
GNB = GaussianNB()
GNB.fit(X_train, y_train)
predictions = GNB.predict(X_test)
#the output score comes to be 0.74401
#model11 - SVC, support vector classifier
from sklearn.svm import SVC
SVC = SVC()
SVC.fit(X_train, y_train)
predictions = SVC.predict(X_test)
#the output score comes to be 0.6698
#model12 - Linear SVC
from sklearn.svm import LinearSVC
LinSVC = LinearSVC()
LinSVC.fit(X_train, y_train)
predictions = LinSVC.predict(X_test)
#the output score comes to be 0.770334
#model13 - perceptron ,equivalent to SGDClassifier(loss=”perceptron”, eta0=1, learning_rate=”constant”, penalty=None)
from sklearn.linear_model import Perceptron
per = Perceptron()
per.fit(X_train, y_train)
predictions = per.predict(X_test)
#the output score comes to be 0.75358
#creating confusion matrix and using different threshold for predictions
from sklearn.metrics import confusion_matrix
confusion_matrix(actualpredictions, predictions, labels=[0,1])#if labels = [1,0] the values will be swapped
#create a proper confusion matrix
pd.DataFrame(confusion_matrix(actualpredictions, predictions, labels=[1,0]), columns=[0,1], index=[0,1])
#columns are actual values and rows are predicted values
#e.g. 0,0 (first col first row) means how many are actually 0 and also we predicted 0, 0,1 how may are are actually 0 and how many we predicted 1
#now what logistic regression actually does prediction is based on probabilities, it calculated probabilities and then assigns 1 to values with prob>0.5 and 0 to other values
#also there are other models which predicts probabilitiesm but here we will use logostic regression
#to get probabilities
LogR.predict_proba(X_test)#this will give us two row, first is the probability of 0 and second column is the probability for 1, we only need second column
probs = LogR.predict_proba(X_test)
probs = probs[:,1]
#we can get the default numpy predictions in a couple of ways
defaultLogisticPredictions1 = (probs>0.5).astype('int32')
defaultLogisticPredictions2 = np.where(probs>0.5,1,0)
np.array_equal(defaultLogisticPredictions1,defaultLogisticPredictions2)#both are same
accuracy_score(actualpredictions, defaultLogisticPredictions1)#also the accuracy score we can check and it matched the logistic regression predictions
#we can use different threshold for prediction
predictionUsingDiffThreshold = (probs>0.6).astype('int32')#using threshold of 0.6 instead of default 0.5
accuracy_score(actualpredictions, predictionUsingDiffThreshold)#after calculating i noticed that the accuracy_score actually slightly increased
#first time crossed 80% on kaggle with titanic data set
#** i am using the original test labels for testing my model before posting to kaggle as kaggle has only 10 submission/day, i am not using it for training
#roc curve and roc auc score
from sklearn.metrics import roc_auc_score
roc_auc_score(actualpredictions, probs)#this will give you AUC score for an ROC curve
#ROC curve is a curve between TPR(y axis) and FPR(x axis) for different values of threshold from 0 to 1, a perfect binary classifier will have an roc_auc_score=1
#TPR is also called sensitivity or recall and is given by TP/(TP + FN), FPR=1-specificity(where specificity=TNR=TN/(TN+FP))
#for plotting ROC curve
from sklearn.metrics import roc_curve
tpr, fpr, thresholds = roc_curve(actualpredictions, probs)#roc_curve return three values, tpr, fpr, and thresholds
#you can use these values also to calculate roc auc score
from sklearn.metrics import auc
auc(tpr, fpr)#it is same as roc_auc_score(actualpredictions, probs)
#to plot ROC curve we can do as below
plt.plot(tpr, fpr)
plt.plot([0,1],[0,1])
plt.show()
#also we can do some fancy plotting
plt.plot(tpr, fpr)
plt.plot([0,1],[0,1], c='r')#create diagonal line
plt.plot([0,1],[0,0], c='k')#this and below three lines are to create a square boundry
plt.plot([0,0],[0,1], c='k')
plt.plot([1,0],[1,1], c='k')
plt.plot([1,1],[0,1], c='k')
plt.fill_between(tpr, fpr, color='r', alpha=0.3)#fill area between the curve and the x axis, this is auc
datapoints = list(zip(tpr[::25],fpr[::25],thresholds[::25]))#to get the threshold of few data points
for i in range(len(tpr[::25])):
plt.text(datapoints[i][0],datapoints[i][1],round(datapoints[i][2],2))#plotting those thresolds to get an idea
plt.show()
#plotting decision trees (you can only plot the decison tree, not any ensemble tree)
from sklearn.tree import DecisionTreeClassifier
Detree = DecisionTreeClassifier()
Detree = Detree.fit(X_train, y_train)
predictions = Detree.predict(X_test)
from sklearn.tree import export_graphviz#this is used to save the tree to a dot file
export_graphviz(Detree, out_file='dtree.png', rounded = True, proportion = False, precision = 2, filled = True)
#now you need to covert dot file to png or jpeg then you can use it to see the tree structure
#important features, feature importance
#for RandomForest and other tree based classifier
importances = RandF.feature_importances_#this will give you the features and their importance
indices = np.argsort(importances)#we sort the indices based on values
importanceSeries = pd.Series(importances[indices], list(X_train.columns[indices]))#create a series of the importance feature
importanceSeries.plot(kind='bar')#we are plotting the above series
plt.show()
#for logistic regression, we can use the coefficient values to check which all features are important
#one thing we can do is by multiplying the coefficient by standard deviations
pd.Series(abs(np.std(X_train, 0)*LogR.coef_.flatten())).sort_values(ascending=False)
#also instead of doing the above you can fit the model on standarized parameters
#or you can fit the Generalized linear model from statsmodel and use the p values
import statsmodels.api as sm
LogGLM = sm.GLM(y_train,X_train,data=trainData, family=sm.families.Binomial())#family binomial mean logistic or binary model
result = LogGLM.fit()
print(result.summary())#it will print R style summary
#from summary you can check the p values of the variable if the p value < 0.05 the variable is important
#creating an ensemble of classifiers and using simple voting to predict the output
#here i will use 5 of the best performing models from above
from sklearn.ensemble import VotingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from xgboost import XGBClassifier
from sklearn.svm import LinearSVC
from sklearn.naive_bayes import GaussianNB
modl1 = LogisticRegression()
modl2 = RandomForestClassifier()
modl3 = XGBClassifier()
modl4 = LinearSVC()
modl5 = GaussianNB()
vClassifier = VotingClassifier(estimators=[('lor', modl1),('rf', modl2),('xgb', modl3),('svc', modl4),('gnb', modl5)],voting='hard')#hard means do majority voting
vClassifier.fit(X=X_train, y=y_train)
votingPrediction = vClassifier.predict(X=X_test)
accuracy_score(actualpredictions, votingPrediction)#accuracy is better than most individual score but still less conpared to logistic with threshold 0.65071
#cross validation
#we use cross validation to get an estimate of how the model will perform on test data
#usually we divide out train data into k parts and use k-1 parts for training and 1 part for testing and this is done k number of times
#k number of times means each of the k part is treated as test once and remaining data is used for training
#we have libraries in sklearn which will do this automatically and give us the output result
from sklearn.model_selection import cross_val_score
modl1 = LogisticRegression()#our model
scores = cross_val_score(modl1, X_train, y_train, cv=10)#10 fold cross validation
print(scores)
print("Accuracy: %0.2f (+/- %0.2f)" % (scores.mean(), scores.std() * 2))#print average and standard deviation
print("Accuracy: {:.2f} (+/- {:.2f})".format(scores.mean(), scores.std() * 2))#same as above just using .format
#also you can use
from sklearn.model_selection import cross_validate#from this you have to explicitly get the scores
cv_results = cross_validate(modl1, X_train, y_train, cv=10)
cv_results['test_score']#to get the scores, same as scores above
#grid search
#estimators have many hyperparameter which are set to some default values, we can change these values as per our need
#for example in logistic regression we want to give different weight to 1 then 0, so our algorithm will try to correct more 1's compared to 0's
#in random forest we can let tree grow a little bit more depending on some criterian, or in svm we can use different kernels
#we can do all of these things manually but there are so many combination and it will be a headache, so we have Grid Search CV to the rescue
#grid search cv will fit our models for all the combinations of the parameters which we give and also do crossvalidation to test the score
#based on this score it choses which parameter combination is better
#here we will use randomforest classifier to demonstrate this
from sklearn.model_selection import GridSearchCV
parameters = {'n_estimators':[5,7,9,11,13],'criterion':['gini','entropy'],'min_samples_split':[2,4,6,8]}#parameters to do grid search on
RandF = RandomForestClassifier()
GridS = GridSearchCV(RandF, parameters, cv=10)#using 10 fold cross validation with grid search
GridS.fit(X_train, y_train)
GridS.best_estimator_#will give you the best estimator with the best parameter combination
RandFBest = GridS.best_estimator_#you can assign that to a variable
RandFBestPredictions = RandFBest.predict(X_test)#we can use the best_estimator_ to do our predictions
#in my case doing GridSearchCV increased my test accuracy with 1 percent, its just an demonstrating example, you can use this with different algos and different parameters
#creating a correlation matrix and making it easy to read
cols = Data.columns.values#get all the columns on which you want to do the correlation, it can be all the columns or only given columns
#cols = ['col1','col2' etc], you can do like this also
corrMatrix = Data.corr()#it will create a correlation matrix
threshold = 0.5#you can define any threshold, here i want to see all the pairs whose abs correlation value is >=0.5
corr_list = []#create an empty list in which we will store the values
for i in range(10):
for j in range(i+1, 10):#i+1 as we dont want to repeat the same pair again and again as corr(i,j) is same as corr(j,i)
if (data_corr.iloc[i, j] >= 0.5 and data_corr.iloc[i, j] < 1) or (data_corr.iloc[i, j] <= -0.5 and data_corr.iloc[i, j] > -1):
corr_list.append([data_corr.iloc[i, j], i, j])
print(corr_list)#this list is having correlation value and the row index and column index of the variable
sorted_corr_list = sorted(corr_list, key=lambda x: -abs(x[0]))#sorting the correlation matrix based on first value (correlation value) of each row, not on the indices
print(sorted_corr_list)
#now to properly print the correlation values with the columns names instead of indices
for v, i, j in sorted_corr_list:
print('{} and {} = {:.2f}'.format(cols[i], cols[j], v))#cols is the list of columns we declared earlier
#plotting decision trees (you can only plot the decison tree, not any ensemble tree)
from sklearn.tree import DecisionTreeClassifier
Detree = DecisionTreeClassifier()
Detree = Detree.fit(X_train, y_train)
predictions = Detree.predict(X_test)
from sklearn.tree import export_graphviz#this is used to save the tree to a dot file
export_graphviz(Detree, out_file='dtree.png', rounded = True, proportion = False, precision = 2, filled = True)
#now you need to covert dot file to png or jpeg then you can use it to see the tree structure
#important features, feature importance
#for RandomForest and other tree based classifier
importances = RandF.feature_importances_#this will give you the features and their importance
indices = np.argsort(importances)#we sort the indices based on values
importanceSeries = pd.Series(importances[indices], list(X_train.columns[indices]))#create a series of the importance feature
importanceSeries.plot(kind='bar')#we are plotting the above series
plt.show()
#for logistic regression, we can use the coefficient values to check which all features are important
#one thing we can do is by multiplying the coefficient by standard deviations
pd.Series(abs(np.std(X_train, 0)*LogR.coef_.flatten())).sort_values(ascending=False)
#also instead of doing the above you can fit the model on standarized parameters
#or you can fit the Generalized linear model from statsmodel and use the p values
import statsmodels.api as sm
LogGLM = sm.GLM(y_train,X_train,data=trainData, family=sm.families.Binomial())#family binomial mean logistic or binary model
result = LogGLM.fit()
print(result.summary())#it will print R style summary
#from summary you can check the p values of the variable if the p value < 0.05 the variable is important
#creating an ensemble of classifiers and using simple voting to predict the output
#here i will use 5 of the best performing models from above
from sklearn.ensemble import VotingClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from xgboost import XGBClassifier
from sklearn.svm import LinearSVC
from sklearn.naive_bayes import GaussianNB
modl1 = LogisticRegression()
modl2 = RandomForestClassifier()
modl3 = XGBClassifier()
modl4 = LinearSVC()
modl5 = GaussianNB()
vClassifier = VotingClassifier(estimators=[('lor', modl1),('rf', modl2),('xgb', modl3),('svc', modl4),('gnb', modl5)],voting='hard')#hard means do majority voting
vClassifier.fit(X=X_train, y=y_train)
votingPrediction = vClassifier.predict(X=X_test)
accuracy_score(actualpredictions, votingPrediction)#accuracy is better than most individual score but still less conpared to logistic with threshold 0.65071
#cross validation
#we use cross validation to get an estimate of how the model will perform on test data
#usually we divide out train data into k parts and use k-1 parts for training and 1 part for testing and this is done k number of times
#k number of times means each of the k part is treated as test once and remaining data is used for training
#we have libraries in sklearn which will do this automatically and give us the output result
from sklearn.model_selection import cross_val_score
modl1 = LogisticRegression()#our model
scores = cross_val_score(modl1, X_train, y_train, cv=10)#10 fold cross validation
print(scores)
print("Accuracy: %0.2f (+/- %0.2f)" % (scores.mean(), scores.std() * 2))#print average and standard deviation
print("Accuracy: {:.2f} (+/- {:.2f})".format(scores.mean(), scores.std() * 2))#same as above just using .format
#also you can use
from sklearn.model_selection import cross_validate#from this you have to explicitly get the scores
cv_results = cross_validate(modl1, X_train, y_train, cv=10)
cv_results['test_score']#to get the scores, same as scores above
#grid search
#estimators have many hyperparameter which are set to some default values, we can change these values as per our need
#for example in logistic regression we want to give different weight to 1 then 0, so our algorithm will try to correct more 1's compared to 0's
#in random forest we can let tree grow a little bit more depending on some criterian, or in svm we can use different kernels
#we can do all of these things manually but there are so many combination and it will be a headache, so we have Grid Search CV to the rescue
#grid search cv will fit our models for all the combinations of the parameters which we give and also do crossvalidation to test the score
#based on this score it choses which parameter combination is better
#here we will use randomforest classifier to demonstrate this
from sklearn.model_selection import GridSearchCV
parameters = {'n_estimators':[5,7,9,11,13],'criterion':['gini','entropy'],'min_samples_split':[2,4,6,8]}#parameters to do grid search on
RandF = RandomForestClassifier()
GridS = GridSearchCV(RandF, parameters, cv=10)#using 10 fold cross validation with grid search
GridS.fit(X_train, y_train)
GridS.best_estimator_#will give you the best estimator with the best parameter combination
RandFBest = GridS.best_estimator_#you can assign that to a variable
RandFBestPredictions = RandFBest.predict(X_test)#we can use the best_estimator_ to do our predictions
#in my case doing GridSearchCV increased my test accuracy with 1 percent, its just an demonstrating example, you can use this with different algos and different parameters
#creating a correlation matrix and making it easy to read
cols = Data.columns.values#get all the columns on which you want to do the correlation, it can be all the columns or only given columns
#cols = ['col1','col2' etc], you can do like this also
corrMatrix = Data.corr()#it will create a correlation matrix
threshold = 0.5#you can define any threshold, here i want to see all the pairs whose abs correlation value is >=0.5
corr_list = []#create an empty list in which we will store the values
for i in range(10):
for j in range(i+1, 10):#i+1 as we dont want to repeat the same pair again and again as corr(i,j) is same as corr(j,i)
if (data_corr.iloc[i, j] >= 0.5 and data_corr.iloc[i, j] < 1) or (data_corr.iloc[i, j] <= -0.5 and data_corr.iloc[i, j] > -1):
corr_list.append([data_corr.iloc[i, j], i, j])
print(corr_list)#this list is having correlation value and the row index and column index of the variable
sorted_corr_list = sorted(corr_list, key=lambda x: -abs(x[0]))#sorting the correlation matrix based on first value (correlation value) of each row, not on the indices
print(sorted_corr_list)
#now to properly print the correlation values with the columns names instead of indices
for v, i, j in sorted_corr_list:
print('{} and {} = {:.2f}'.format(cols[i], cols[j], v))#cols is the list of columns we declared earlier
#Grid search for too many parameter combination might take too much time, so instead we can use randomized search cv
from sklearn.model_selection import RandomizedSearchCV
#works in a similar way as gridsearch cv
#validation curve
#this curve shows training vs cross validation score for different values of the parameters, below is the scikit learn link
https://scikit-learn.org/stable/auto_examples/model_selection/plot_validation_curve.html#sphx-glr-auto-examples-model-selection-plot-validation-curve-py
#learning curve
#this will show the training and cross val score wrt to number of training examples-model-selection-plot-validation-curve-py
https://scikit-learn.org/stable/auto_examples/model_selection/plot_learning_curve.html#sphx-glr-auto-examples-model-selection-plot-learning-curve-py
#image segmentation using k-means, we can use mean shift but it will take too much time if you don't have a good enough system
import matplotlib.image as mpimg#to see image
img=mpimg.imread(imgspath)
imgplot = plt.imshow(img)#show image
plt.show()
#create a dataframe from the image after creating a 2d array from a 3d array (colored images are generally 3d arrays)
imageFrame = pd.DataFrame(img.transpose(2,0,1).reshape(3,-1).transpose(), columns=['red', 'green', 'blue'])
#also you can use img.reshape(x*y, z) to reshape the array and then do km.fit(img.reshape(x*y, z))
from sklearn.cluster import KMeans
km = KMeans(n_clusters=8)
km.fit(imageFrame)
cluster_centers = km.cluster_centers_
cluster_labels = km.labels_
x, y, z = img.shape
plt.imshow(cluster_centers[cluster_labels].reshape(x, y, z))
plt.show()
#one hot encoding and Label Binarizer
from sklearn.preprocessing import OneHotEncoder
encoder = OneHotEncoder()
housing_cat_1hot = encoder.fit_transform(housing_cat_encoded.reshape(-1,1))
#the above code will create a sparse matrix, which will only store the position of non zero element
#to convert to dense matrix you can use
housing_cat_1hot.toarray()
#the above two operations can be combined in one using Label Binarizer
from sklearn.preprocessing import LabelBinarizer
encoder = LabelBinarizer()
housing_cat_1hot = encoder.fit_transform(housing_cat)
#You can get a sparse matrix instead by passing sparse_output=True to the LabelBinarizer constructor
#pipelines
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import Imputer
num_pipeline = Pipeline([('imputer', Imputer(strategy="median")),
('attribs_adder', CombinedAttributesAdder()),#here CombinedAttributesAdder is a custom transformer
('std_scaler', StandardScaler()),])
#All but the last estimator must be transformers (i.e., they must have a fit_transform() method). The names can be anything you like.
#custom transformer
from sklearn.base import BaseEstimator, TransformerMixin
class DataFrameSelector(BaseEstimator, TransformerMixin):#this transformer we can use as a first thing in pipeline
def __init__(self, attribute_names):#as we need not apply transformation on all the columns, so you can give specific columns which
self.attribute_names = attribute_names#will get filtered out in the first step
def fit(self, X, y=None):
return self
#You will want your transformer to work seamlessly with Scikit-Learn functionalities
#(such as pipelines), and since Scikit-Learn relies on duck typing (not inheritance),
#all you need is to create a class and implement three methods: fit()
#(returning self), transform(), and fit_transform(). You can get the last one for
#free by simply adding TransformerMixin as a base class.
#we can use the above trasnformer as below
num_attribs = list(columns we need to be transformed)
num_pipeline = Pipeline([
('selector', DataFrameSelector(num_attribs)),#this will only pass those specific columns to the next step
('imputer', Imputer(strategy="median"))
('attribs_adder', CombinedAttributesAdder()),
('std_scaler', StandardScaler()),])
num_pipeline.fit_transform(data)#or if you dont want to do the DataFrameSelector step you can only pass the small dataframe with specific columns
#loading or creating data using sklearn datasets
from sklearn.datasets import fetch_mldata
mnist = fetch_mldata('MNIST original')#this is loading mnist dataset
X, y = mnist["data"], mnist["target"]
#get function source code
#sometimes you want to know what's going on in a function if you import it like we did in above case
#we can use inspect module for checking that
import inspect
lines = inspect.getsource(fetch_mldata)
print(lines)
#stratified K Fold
from sklearn.model_selection import StratifiedKFold
skfolds = StratifiedKFold(n_splits=3, random_state=42)
for train_index, test_index in skfolds.split(X_train, y_train_5):
#do sometehing like create a train and test set using the indexes and do fit predict and check the scores
#to create your own estimator
from sklearn.base import BaseEstimator#this estimator has a fit method which does nothing and a predict method which will always return 0
class Never5Classifier(BaseEstimator):
def fit(self, X, y=None):
pass
def predict(self, X):
return np.zeros((len(X), 1), dtype=bool)
#one vs one and one vs all
#generally classifiers when doing multiclass classifications use one vs all except one vs one(for svm as it does not scale well)
#to force a classifier to use one vs one we can do like below
from sklearn.multiclass import OneVsOneClassifier
ovo_clf = OneVsOneClassifier(SGDClassifier(random_state=42))#here we pass the estimator inside the OneVsOneClassifier
#** trees don't need to do one vs one or one vs all as they are by default capable of doing multiclass classification
#KNeighborsClassifier (KNN) supports multilabel classification, but not all classifiers do
#simple noise reduction algo, using mnist dataset, its part of algos called multioutput algo, ie. each label can have more than 2 possible values
#when the label has 2 possible values its called multiclass algo
#X_train is the training data, X_test is the testing data
train_noise = np.random.randint(0, 100, (len(X_train), 784))#creting some noise in the shape of train data
test_noise = np.random.randint(0, 100, (len(X_test), 784))#similar for test data
X_train_mod = X_train + train_noise#adding noise to train data which will be used for training
X_test_mod = X_test + test_noise#adding noise to test data, will use for testing
y_train_mod = X_train#training labels (y) is the clean train data
from sklearn.neighbors import KNeighborsClassifier#as KNN is capable of multioutput multiclass classification
KNN = KNeighborsClassifier()
KNN.fit(X_train_mod, y_train_mod)
clean_digit = KNN.predict([X_test_mod[0]])#predicting/cleaning the first digit from test set
#now plotting to see the difference
fig, ax = plt.subplots(1,3)#creating a 1X3 grid
import matplotlib as mpl
ax[0].imshow(clean_digit.reshape(28,28), cmap=mpl.cm.binary)#cleaned digit
ax[1].imshow(X_test_mod[0].reshape(28,28), cmap=mpl.cm.binary)#noisy digit
ax[2].imshow(X_test[0].reshape(28,28), cmap=mpl.cm.binary)#original digit
plt.show()
#solution to linear regression
#1. using normal equation
#when you write in matrix form y=x.m, y is column vector, x is a matrix whose first column is 1 and other rows are each features,
#and m is again a column vector of coefficients where first element is the bias term
#here . is dot product
#y=x.m, we multiply both side with xt which is transpose of x, xt.y=xt.x.m, as xt.x is to make the matrix square,
#bringing xt.x to left side, inv(xt.x).xt.y=m, this is called normal equation
#first create a dummy data
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
from sklearn.linear_model import LinearRegression
lg = LinearRegression()
lg.fit(X, y)
print(lg.intercept_, lg.coef_)#use linear regression to get the model parameters
#now check if the result are close as above using linear regression
X_new = np.c_[np.ones((100, 1)), X]#creating new X, adding onee as first row for bias term
theta = np.linalg.inv(X_new.T.dot(X_new)).dot(X_new.T).dot(y)#normal equation
print(theta)#you can check thetas are quite/nearly equal with linear regression model
#The computational complexity of inverting such a matrix is typically about O(n2.4) to O(n3) (depending on the implementation). In
#other words, if you double the number of features, you multiply the computation time by roughly 22.4 = 5.3 to 23 = 8.
#The Normal Equation gets very slow when the number of features grows large (e.g., 100,000).
#On the positive side, this equation is linear with regards to the number of instances in
#the training set (it is O(m)), so it handles large training sets efficiently, provided they can fit in memory.
#batch gradient descent
#now if we want to train too many features and we dont have too much ram, gradient descent comes into picture
#When using Gradient Descent, you should ensure that all features have a similar scale
#(e.g., using Scikit-Learn’s StandardScaler class), or else it will take much longer to converge.
#in gradient descent we take gradient (partial differentiation) across all the parameter and simultaneous update the theta'same
#you can search for gradient descent on google if you dont know it
eta = 0.1 #learning rate, how big/small steps we want to take in updating the parameters
n_iterations = 1000#for how many iteration to run the gradient descent, we can also use threshold values
m = 100#number of data points, we will divide the cost function by m as to normailize it as the cost value should not be affected by m
theta = np.random.randn(2,1)#random initialization of theta's
#the algorithm
for iteration in range(n_iterations):
gradients = 2/m * X_new.T.dot(X_new.dot(theta) - y)#as you parital differentiate the cost function wrt various parameter you get this simple set of
theta = theta - eta * gradients #equations which you can represnt using linear algebra, and in this step we are updating theta'same
#To find a good learning rate, you can use grid search
#for chossing no of iteration we can chose a large number but the loop should break if the changes in theta's for two consecutive iteration is less than
#some threshold value which we can chose
#stochastic gradient descent **can be implemeted as out of core learning (when data does not fits in the memory)
#The main problem with Batch Gradient Descent is the fact that it uses the whole training set to compute the gradients at every step,
#which makes it very slow when the training set is large.
#On the other hand, due to its stochastic (i.e., random) nature, this algorithm is much less regular than Batch Gradient Descent
#When the cost function is very irregular (as in Figure 4-6), this can actually help the algorithm jump out of local minima,
#so Stochastic Gradient Descent has a better chance of finding the global minimum than Batch Gradient Descent does
#Therefore randomness is good to escape from local optima, but bad because it means that the algorithm can never settle at the minimum.
#One solution to this dilemma is to gradually reduce the learning rate, This process is called simulated annealing
n_epochs = 50
t0, t1 = 5, 50 #learning schedule hyperparameters
def learning_schedule(t):#for reducing learning rate, at every iteration t increase so the return value decreases
return t0 / (t + t1)#you can define your own functions
theta = np.random.randn(2,1)#random initialization
for epoch in range(n_epochs):
for i in range(m):
random_index = np.random.randint(m)
xi = X_new[random_index:random_index+1]
yi = y[random_index:random_index+1]
gradients = 2 * xi.T.dot(xi.dot(theta) - yi)
eta = learning_schedule(epoch * m + i)
theta = theta - eta * gradients
#for plotting how we get to the final parameters you can use below code, you can do similar with batch gradient descent
n_epochs = 50
t0, t1 = 5, 50 # learning schedule hyperparameters
def learning_schedule(t):
return t0 / (t + t1)
theta = np.random.randn(2,1) # random initialization
theta1=[theta[0]]#creating a list of theta1's
theta2=[theta[1]]#creating a list of theta2's
for epoch in range(n_epochs):
for i in range(m):
random_index = np.random.randint(m)
xi = X_new[random_index:random_index+1]
yi = y[random_index:random_index+1]
gradients = 2 * xi.T.dot(xi.dot(theta) - yi)
eta = learning_schedule(epoch * m + i)
theta = theta - eta * gradients
theta1.append(theta[0])#appending the new values
theta2.append(theta[1])
plt.plot(theta1, theta2, lw=0.5, marker='o', ms=1)#creating a line plot with markers
plt.show()
#polynomial regression
#you can extend your linear model to include quadratic terms
m = 100
X = 6 * np.random.rand(m, 1)-3
y = 0.5 * X**2 + X + 2 + np.random.randn(m, 1)
plt.scatter(X, y, s=5)#to see the data
plt.show()
from sklearn.preprocessing import PolynomialFeatures
poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)#transforming into polynomial features
lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)#fitting the model with poly features
lin_reg.intercept_, lin_reg.coef_#as we now have two features one for x and other for x^2, so we here will have two intercepts
#you can plot to see the predicted line
y_preds = lin_reg.intercept_ + X*lin_reg.coef_[:,0] + X**2*lin_reg.coef_[:,1]
plt.scatter(X, y, s=5)
plt.scatter(X, y_preds, s=2)
plt.show()
#**PolynomialFeatures adds all combinations of features up to the given degree,
#e.g. PolynomialFeatures with degree=3 would not only add the features a^2, a^3, b^2, and b^3, but also the combinations ab, a^2b, and ab^2
#if you keep increasing the degree of polynomials you will fit the data more perfectly and this is called overfitting
#for e.g. if you fit a simple linear model to above data it wont fit properly as we clearly saw the relationship is not linear, its called underfitting
#regularization
#as we saw above we have to have a tradeoff between overfitting(variance) and underfitting(bias)
#this is when regularization comes into picture
#the idea is to create a complex (overfitted) model and then reduce the weights(slopes) of the parameters
#here we define a new cost function :
#which is old cost function(i.e. mean squared error) and sum of squared parameter values (ridge) or sum of absolute parameter values (lasso)
#lasso - Least Absolute Shrinkage and Selection Operator Regression
#so if we make the model more complex generally we keep increasing the parameter values but increasing so will increase the second term of the cost function
#so we need to find a sweet spot in between
#**ridge can only make parameter values smaller, but lasso can make them as zero also which means lasso can work also as feature selector
#ridge regression
#we can solve ridge regression using normal equation also
theta = np.linalg.inv(X_new.T.dot(X_new) + α*A).dot(X_new.T).dot(y)#here A is an identity matrix with first term as 0 instead of 1-abs
#the first term is zero as we don't regularize the bias term, The hyperparameter α controls how much you want to regularize the model
#Elastic net
#Elastic Net is a middle ground between Ridge Regression and Lasso Regression.
#The regularization term is a simple mix of both Ridge and Lasso’s regularization terms
#** so you may ask where to use lasso or ridge or elastic net
#It is almost always preferable to have at least a little bit of regularization, so generally you should avoid plain Linear Regression.
#Ridge is a good default, but if you suspect that only a few features are actually useful, you should prefer Lasso
#or Elastic Net since they tend to reduce the useless features’ weights down to zero as we have discussed.
#Early Stopping
#A very different way to regularize iterative learning algorithms such as Gradient Descent is to stop training
#as soon as the validation error reaches a minimum. This is called early stopping
#logistic regression - binary classifier
#is is defined as y = sigmoid(theta.X)
#here also we solve for the parameters of the sigmoid function, and for that we have to define a cost function
#our objective is to predict 0 or 1, so our cost function should decrease if we predict value close to 0 if actual is 0 and vice verse and same for 1.
#now sigmoid function is basically gives output in terms of probabilities are it is defined as 1/(1+e^-(theta.x))
#as x tends to infinity this function tends to 1 and if x tends to -infinity it tends to 0, so we always get a value between 0 and 1 including both
#we define our cost function as -1/m.summation(y.log(p) + (1-y)log(1-p)), when y=1 this function becomes -1/m.log(p), and similar for y=0.
#here p is the probability or output of the signmoid fucntion, and you can see the graph of log(x) and log(1-x) for why this function makes sense
#here we don't have any closed form or normal equation as exponential comes into picture and we can't solve this using linear algebra
#but the good news is this cost function is convex so we can use gradient descent.
#also there is another way called maximum likelihood estimation
#how we make predictions using logistic regression, as we get probabilities as output by default we predict 1 if p>=0.5 and 0 otherwise.
#the decision boundry is defined by the power of the exponential, if theta.X>=0, we get p>=0.5 and 0 otherwise,
#now as we can see the power of e is actually the same equation as that of linear regression, that's why logistic regression is also an linear model
#draw the decision boundry (for two variable)
#when we have two explanatory variables, the decison boundry is a line, which we can easily draw
from sklearn import datasets
iris = datasets.load_iris()#loading iris dataset
iris_data = iris.data[:,2:]#taking out the last two columns which we will use for training
log_r = LogisticRegression()
iris_y = (iris["target"] == 2).astype(np.int)#just keeping only one type of iris,so its a binary problem
log_r.fit(iris_data,iris_y)
plt.figure(figsize=(8, 4), dpi=80)
plt.scatter(iris.data[:,2],iris.data[:,3],s=5, c=iris_y, marker='*', cmap='prism')#plotting the data
ax=plt.gca()#getting current axis
y_vals = np.array(ax.get_ylim())#getting the y limits of the previous plot
x_vals = -(y_vals * log_r.coef_[0][1] + log_r.intercept_[0])/log_r.coef_[0][0]#getting the coefficient and intercepts from the model
plt.plot(x_vals, y_vals, '--', c='k')#plotting the line
plt.xlim(3,7)#limiting the axis to see more clearly, in your case you might have to limit different axis and different range
plt.show()
#you can draw some more fancy plots, which you can find from scikit learn or matplotlib website
#if we have more than 2 classes we can use softmax regression without having to use onevsone or onevsall approach
#in scikit learn you can use it sometehing like this
softmax_reg = LogisticRegression(multi_class="multinomial",solver="lbfgs", C=10)#C can be different
#support vector machine - classification
#works on large margin intution, which is for binary classifier we create a decision boundry which seperates the data in such a way that
#the margin between the nearest data point to the boundry for each of the classes is maximum
#support vectors are the margin vectors not the decision boundry
#**SVMs are sensitive to the feature scales
#soft margin classification - If we strictly impose that all instances be off the street and on the right side, this is
#called hard margin classification. There are two main issues with hard margin classification.
#First, it only works if the data is linearly separable, and second it is quite sensitive to outliers
#The objective is to find a good balance between keeping the street as large as possible and limiting the margin violations
#This is called soft margin classification.
#in svm we have two main hyperparameters C and gamma, smaller the C large the street (margins) and more the violations and vice verse
#similar if gamma is small the farther points define the decision boundry and vice verse, increasing gamma makes the decision boundry irregular (overfit)
#the gamma acts like a regularization parameter
#for linear seperable data, linear svm works well, but for non-linear data either we can add polynomial feature which can work well,
#but sometimes data is too complex and we have to many polynomial feature and the algorithm might become very slow,
#so here we use sometehing called kernel trick, It makes it possible to get the same result as if you added many polynomial features,
#even with very highdegree polynomials, without actually having to add them
#example
SVC(kernel="poly", degree=3, coef0=1, C=5)#here we are using kernel as poly with 3 degrees
#The hyperparameter coef0 controls how much the model is influenced by highdegree polynomials versus low-degree polynomials.
#Another technique to tackle nonlinear problems is to add features computed using a similarity function
#that measures how much each instance resembles a particular landmark.
#similar to polynomial feature we can use kernel trick for similarity functions also, here's an example using RBF(a similarity function)
SVC(kernel="rbf", gamma=5, C=0.001)
#**With so many kernels to choose from, how can you decide which one to use? As a rule of thumb, you should always try the linear
#kernel first (remember that LinearSVC is much faster than SVC(kernel="linear")), especially if the training set is very large or if it
#has plenty of features. If the training set is not too large, you should try the Gaussian RBF kernel as well; it works well in most cases.
#Then if you have spare time and computing power, you can also experiment with a few other kernels using cross-validation and grid
#search, especially if there are kernels specialized for your training set’s data structure.
#solving for svm parameters is a quadratic constrained problem which we can solve using quadratic programming solver.
#svm - regression
#svm also supports linear and nonlinear regression. The trick is to reverse the objective: instead of trying to fit the largest possible
#street between two classes while limiting margin violations, SVM Regression tries to fit as many instances as possible on the street
#while limiting margin violations
#regression works in a similar way as classification, you can use kernels in case of non-linear data
#Decision Trees
#like SVM decison trees are versatile algorithms which we can use for both classification and regression, and even multioutput tasks.
#basic idea in decision trees is that you start with a root node which will have all the training examples and then you keep splitting data
#based on some criterions and you keep doing this until you reach some stopping conditions,
#like the last node should have atleast 10 examples (called leaves) etc
#we have to derive a criteria on which to split the nodes or grow the trees, we have error rate, gini index or entropy.
#all the impurity measures are 0 for a pure node (all data is from same class)
#p(k) is the proportion of data in class k, let us say we have k classes
#error rate = 1 - max(p(k))
#gini impurity = summation(k=1 to k)((p(k)(1-p(k)))) = 1 - summation(k=1 to k)(p(k)^2)
#entropy = -summation(k=1 to k)(p(k)*log2(p(k)))
#we usually define a cost function and minimize it to create a optimum algorithm
#here the cost function we use for CART(classification and regression trees) is n(left)/n)*impurity(left)) + (n(right)/n)*impurity(right)
#where n is data points in the parent node, n(left) is data points in left node and impurity(left) is impurity measure of left node, similar for right
#**cart is greedy algorithm, it searches for optimum split at top level and repeats the same
#similar to minimizing the cost function, we can maximize the information gain,
#information gain of a node is impurity at that node - cost aftet the split using that same impurity, a perfect node will have cost = max(p(k))
#information gain or entropy or gini index all does the split on greedy approach.
#one way to do decision tree regularization is to grow the tree to fullest based on one of the above criteria and then prun it based on some criteria.
#or grow the tree only untill some criteria is fulfilled as discussed above like using min_samples_split.
#some instability of decision tree
#Decision Trees love orthogonal decision boundaries (all splits are perpendicular to an axis), which makes them sensitive to training set rotation.
#also Decision Trees are very sensitive to small variations in the training data
#Ensemble Methods - Bagging and Boosting trees
#ensemble means using multple predictors to make a single predictor.
###### Extra things may be useful
#general imports
import pandas as pd
import numpy as np
import matplotlib as mpl
mpl.use('nbAgg')#for using it as inline in jupyter notebook
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels as sm
import seaborn as sns
import geopy.distance as geodist#for calulating geo distance based on lat lons
from scipy import stats, integrate
import os
#if we want to get file path
print(plt.__file__)#here we want to get the path of plt function
#data preprocessing , imputation, scaling
from sklearn.preprocessing import Imputer
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import Normalizer
from sklearn.preprocessing import LabelEncoder
Scaler = StandardScaler()
X_train_Scaled = Scaler.fit_transform(X_train)#use fit transform on training data
X_test_Scaled = Scaler.transform(X_test)#use only transform on test data
#similarly we can do for MinMaxScaler and Normalizer
#different tree based classifier
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.ensemble import RandomForestClassifier
from xgboost import XGBClassifier
from sklearn.tree import DecisionTreeClassifier, export_graphviz
from sklearn.ensemble import AdaBoostClassifier
from sklearn.ensemble import GradientBoostingClassifier
#other imports
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, log_loss
from sklearn.metrics import roc_auc_score
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import Perceptron
from sklearn.linear_model import SGDClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC, LinearSVC
from sklearn.metrics import confusion_matrix
#confusion matrix
labels=[0,1]
cnf_mat = confusion_matrix(predctions, y_originals, labels)#List of labels to index the matrix
#feature importance which we can use for feature selection
#for tree based classifier we can get the feature importance like which of the features are important
#example
model = ExtraTreesClassifier(n_estimators=c-1,max_features=0.5,n_jobs=-1,random_state=seed)#here we defined ExtraTreesClassifier
model.fit(X_train, y_train)#we fitted data
importances = forest.feature_importances_#get all the values from feature_importances_
indices = np.argsort(importances)#we get the sorted indices, means if at zero index we have 2 which means feature 2 is most important
model.feature_importances_.shape#here we can see how many features are there in feature importance it should be equal to the fitted number of columns
f_imp = pd.Series(importances[indices], list(columns[indices]))#we can create a series of feature importance features
f_imp.plot(kind='bar', label='extratreenormal')#we can plot the feature importance to see which is more important feature
plt.legend()
plt.show()
#feature selection using RFE, recursive feature elimination
from sklearn.feature_selection import RFE
estimator = ExtraTreesClassifier(n_estimators=c-1,max_features=0.5,n_jobs=-1,random_state=seed)#here we define an estimator
selector = RFE(estimator, 0.75*(numOfCols))#here we define a selector which will use 75% of all feature which are best feature, If None half of the features are selected
selector = selector.fit(X_train, y_train)#then we use selector to fit the training data
#loading huge data using iterator object, let us say we have some million records we cant load all at once if our system is not capable
#also we want to load only certain data, so loading full data and then filtering is a overhead a better solution
data_temp=pd.read_csv(dataPath, iterator=True, chunksize=1000, usecols['col1','col2','col3'])
data_main=pd.concat([chunk[chunk.col1=2012] for chunk in data_temp])
#what we are doing above is first loading the data using iterator with 1000 rows and few columns and then concatenating the data
#1000 rows at a time also we are only loading those rows where col1=2012
#pickling
import pickle
#with is use as context manager
with open('model.pickle', 'wb') as pick:#create a model.pickle file and open it in write binary mode
pickle.dump(classifier, pick)#dump the classifier into that file
#to load pickle
pkl_file = open('model.pickle', 'rb')
pickle.load(pkl_file)
#get unique count from each column
df.apply(lambda x : x.nunique())
#groupby on multiple cols
c = cast.groupby([cast.year // 10 * 10,'type']).size()#it will create a multilevel index
c.unstack()#we can unstack or pivot the second index a cols using unstack
#convert using astype
df.date = df.date.astype(np.datetime64)
#filling NaN's
df.fillna(' ')#here we are filling NaN's with spaces
#or we can use some method like ffill or bfill
df.col1.fillna(method='bfill')#backward fill, fills the current NaN using the next values
#usually we might miss the few values in the beginnig or last when we use only bfill or ffill, so we generally use one of bfill or ffill first then use the other
#to ignore warnings in jupyter notebook or generally
import warnings
warnings.filterwarnings('ignore')
#display all the columns in jupyter notebook while displaying data
pd.set_option('display.max_columns', None)
#list all the directories in a path
filenames = os.listdir(filepath)
#filter out the csv's from all the files
filenames = [f for f in filenames if f.endswith(".csv")]
#create correlation matrix
df.corr()
#to find skewness
df.skew()
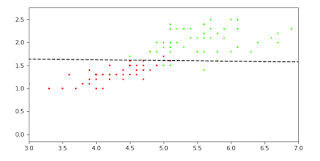
Comments
Post a Comment